Yu. Batrak, R. Batrak, D. Berin, Intellectual Maritime Technologies, UKRAINE
SUMMARY
The propulsion shafting operates at the junction of different media where the interacting conditions change constantly depending on the ship draught, engine speed, ambient and machinery temperature. Once installed on the flexible hull structures it is exposed to hydrodynamic propeller loads, variable contact conditions within the continuous hydrodynamically lubricated elastic bearings. It is obvious that the proper decision concerning of initial linear and angular bearing offsets setting can be made with the help of the computer application only. This paper describes the approach of the computer application based on the most realistic model of the propulsion shafting operation. The procedures for the hull deflections estimation and the propeller hydrodynamic loads calculation are discussed. The special attention is paid to the methods for searching of the optimal linear and angular bearing offsets. Also it is shown that the application of the universal reverse analyses procedure is inevitable for the ships under repair or under renovation.
1. INTRODUCTION
The propulsion machinery mounting is an important stage of the ship construction or repairing because the vital parts of the propulsion shafting such as stern tube bearings, gear boxes and low speed diesel engines are very sensitive to the wrong shaft alignment. Unfortunately neither modern shaft alignment techniques nor the most precise instruments can prevent propulsion train casualties if the shaft alignment design was done without taking into account significant features of the operating conditions.
It is the well-known fact revealed in the 1960-s [1] that the interaction between the main machinery and the environment is one of the main causes of shafting failures. It is clear also that this interaction can’t be taken into account in machinery design properly without the computer application that consider all main factors of the propulsion shafting operations.
There are five main factors connected to the shaft alignment that may affect the propulsion train:
- hull structure deflections caused by the static loads alterations owing to cargo and ballasting operations, as well as by the dynamic loads in a heavy weather;
- thermal growths of the equipment and hull structures;
- excessive wear down of the stern tube bearings;
- propeller hydrodynamic loads because of the thrust eccentricity;
- tooth forces in the case of the geared installations.
First three factors are associated with the changes of bearings space positions, the last two – with the shaft operating loads. Together they define the operating conditions. Various combinations of the operating conditions form the set of the calculation states in which the propulsion train should be proved against the Classification Societies requirements and OEM specifications. The sets of the requirements for the specified calculation states are known as the shaft alignment acceptance criteria.
Violation of the acceptance criteria leads eventually to the equipment failures and the most frequent of them are as the following:
- failure of the main bearings of the low speed engine;
- bearings overheating;
- burning of the aft stern tube bearing;
- fatigue damage of the aft stern tube bearing;
- increased whirling vibration;
- gear teeth damages.
The acceptance criteria have been formed during last fifty years and are based on the computing abilities of that time. Today’s shipbuilding meets new challenges and forces the improvements of the acceptance criteria on the base of the new more sophisticated shaft models and the software tools. The Classification Societies [2], [3] have already started to update the acceptance criteria.
This paper describes the features of the computer application for shaft alignment calculation based on the most realistic model of the propulsion shafting intended to predict and thereby to prevent propulsion shafting failures.
2. SHAFT ALIGNMENT PLAN
The goal of the shaft alignment design is to find the alignment plan (SAP) that satisfies all acceptance criteria in all calculation states. The shaft alignment plan is a set of the bearing space positions relative to the fixed reference line. The space position of the bearings is characterized by the linear and angular offsets in the vertical and in the horizontal planes, Fig. 1.
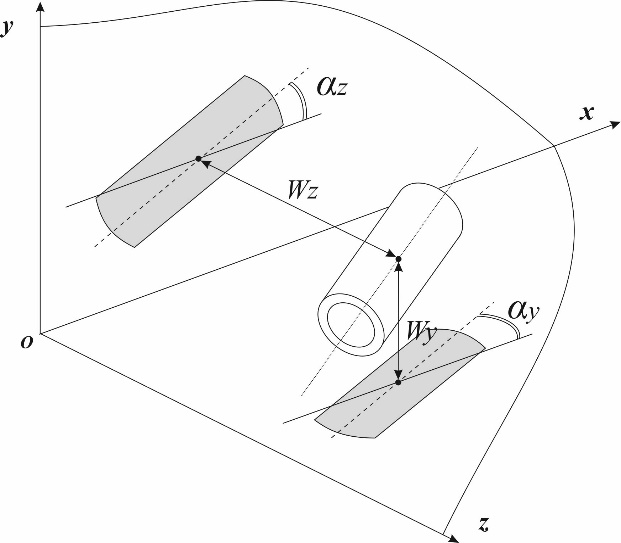
Figure 1: Linear and angular bearing offsets
The shaft alignment plan is not used directly except the procedure of stern tube bearings machining. Usually it is used to define shaft bending parameters such as Sag and Gap at the decoupled flanges, bearing loads, jack-up test diagrams, shaft bending stresses etc.
It is important to note that shaft alignment acceptance criteria are the set of the inequalities, so there is no unique shaft alignment plan. The situation is typical for any design process and shaft designers are forced to search the appropriate solution in the infinite set of the acceptable. This task remains as before some kind of art. The purpose of the software is to facilitate this process and make it more effective and reliable.

Figure 2: The acceptable linear offsets space
Visualization of the space of the acceptable alignment plan solutions is a powerful tool in a decision making process. The sample of the acceptable linear offsets space which was obtained with the Offset Explorer module of the ShaftDesigner package [4] for typical three-bearing propulsion shafting is shown on the Fig. 2.
Usually the acceptable offsets space looks like elongated polyhedron. It may be capacious enough for the installations with directly coupled low speed engine or very narrow in the case of the geared installation. If the acceptance criteria are conflicting the polyhedron doesn’t exist and cannot be built at all.
To find the acceptable bearing offsets shaft designer should take the point within the polyhedron. And then another problem arises: what the point yields the best solution?
The answer depends on the goal that shaft designer takes in mind searching for solution. It may be, for example, the minimum values of the offsets. But more reasonable is to take the solution point in the location that provides maximum safe alignment tolerance.
The safe alignment tolerance value calculated by the Offset Explorer means the maximum deviation δ of the linear bearing offsets that keeps the acceptance criteria not violated. This value is the same for all bearings. It guarantees the compliance with the acceptance criteria while the absolute values of the linear offset deviations are less than tolerance δ. In the case of three bearings safe alignment tolerance zone looks like a cube with the side length 2δ inscribed in polyhedron with the solution point in the center (see Fig. 2). When the shaft line has n bearings (n >3) the tolerance zone can be visualized using 3-D and 2-D sections of n-dimensional polyhedron.
The application has the procedure for searching for the solution with the maximum safe alignment tolerance based on non-linear programming algorithm. User can explore the acceptable offsets space manually to know safe alignment tolerance in any point. This gives an opportunity to find the critical bearings whose offsets influence tolerance zone size.
The optimization process is time consuming and in some cases the solution can’t be found at all. The reason is in complexity of the acceptance criteria that results in goal function sharp changes. The shafting when it is lying freely on the supports with clearance has a lot of stable positions. The sudden changes of the shafting position within the bearings make the goal function abrupt.
3. SHAFT BEARING MODELS
The possibility to vary the bearing models in calculation of shaft alignment plan makes the computer application more flexible. Modern applications for shaft alignment design should provide the following bearing models, Fig. 3:
- simple support;
- bilateral support;
- ring support;
- cylindrical support;
- free shape support.
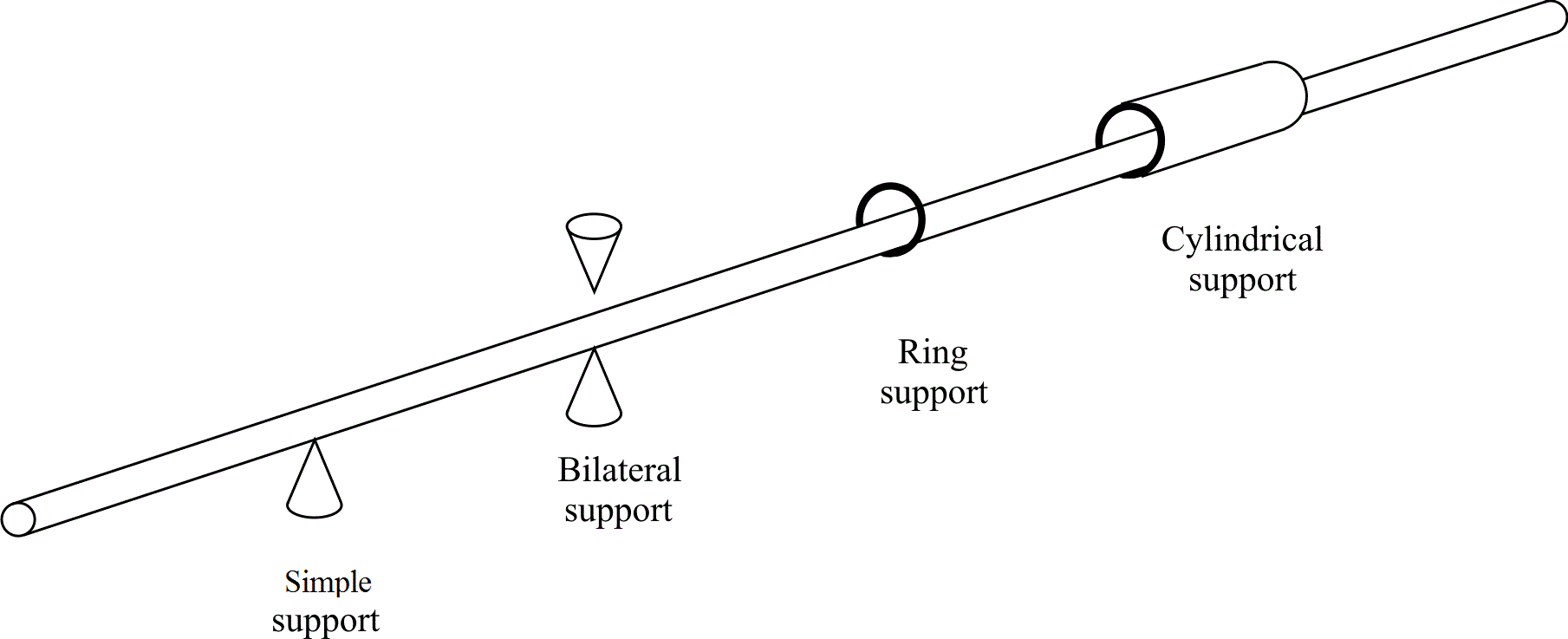
Figure 3: Different approaches for bearing modeling
The choice of the particular model depends on the goals and conditions of the shaft alignment design.
The simple support historically was the first used in the shaft alignment calculations. In spite of the propulsion shafting lies freely on the bearing bush surface, the disconnection of the shaft from the simple support is impossible even in the case of the negative load. For the long and flexible shaft lines it is acceptable because all bearing loads in the most cases are positive and length of the bearing bushes is small relatively to the shaft line length.
For the short and rigid shaft lines the disconnection of the shaft from the bearing lower shell is very possible so bilateral simple support model is more suitable in this case. The bilateral support can bear the negative load after the shaft travelled up for the full bearing diametric clearance and have touched the upper bearing shell.
Two above mentioned models are appropriate if the shaft line bends in the vertical plane only. But the real shaft line owing to the hydrodynamic propeller loads also bends in the horizontal plane. In this case the ring support is to be used. The shaft position within the ring support is defined by the shaft lifting and shifting, Fig. 4.
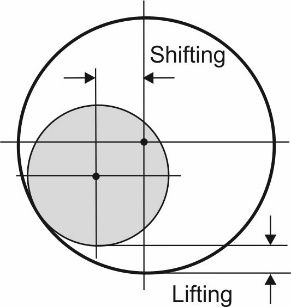
Figure 4: Shaft position within the ring support
The ring support differs fundamentally from the simple and bilateral supports. It imparts the new quality to the shaft bending: vertical and horizontal deformations become coupled because horizontal linear bearing offset causes the shaft lifting.
The first three support models are point wise. The point wise support is a good approximation for the ball and roller bearings but presentation of aft stern tube bearing by the point wise support faces some problems main of them are the difficulty of the support position choice, interpretation and valuation of the calculation results, impossibility to analyze hydrodynamic lubrication of the bearing. These problems can be solved using cylindrical support model. The cylindrical support model yields the results quite different from the results of point wise support and opens the way to the stern tube bearing durability issues study.
The bearing bush internal surface of real non-metal stern tube bearings does not remain cylindrical after a certain time of operation. The bearing bush wear down changes the circular cylinder surface and changes the lubrication conditions significantly. How it influences the bearing operation life still remains an open question. The stern tube bearing bush internal surface may be not a circular cylinder by design (staved bearings, bearings with multiple grooves). For these reasons the support with a free shape of the bush internal surface should be used as the most general model of the stern tube bearings.
First four types of the bearing models are implemented in the ShaftDesigner software. Each subsequent model is more complicated than previous one and requires more computing resources. It is not a problem for a single SAP calculation but becomes critical for the optimization when the thousands plans are tested to find the optimal solution.
The practical usage of ShaftDesigner has shown that the most effective way to design the optimal SAP is to use simple supports to model plain bearings. In this case the acceptable offsets space is exactly the polyhedron the skeleton of which can be easily built.
After all acceptance criteria are satisfied the plain bearings should be turned to the cylindrical supports and the SAP must be checked once again and manually corrected if necessary.
Operating with the angular offsets is still most complicated for the manual correction. Because of the different operating conditions the shaft positions within the bearing bush vary to a large extent especially for the aft stern tube bearing. That’s why it is important to obtain the most appropriate angular offsets to have the best lubrication conditions for the stern tube bearing. ShaftDesigner software provides the special function to select the optimum angular offsets values. After application of this function the final acceptance criteria checking must be made.
4. HULL DEFLECTIONS
Among the operating conditions the hull structure deflections affect the shaft alignment most of all [6]. Bureau Veritas is the first Classification Society that has introduced additional class notation ESA (Elastic Shaft Alignment) this year [2]. First of all it concerns large cargo ships because the draught alteration from the light to ballast condition and from the ballast to full load condition changes the hull deflections significantly. ESA notation is to be assigned to the ships when tail shaft diameter is greater or equal 750 mm and the shaft alignment assessment complies with the specific requirements and methodology.
To calculate hull deflections various modern FEM programs are used. Unfortunately creation of the engine room FEM model still remains very laborious and time-consuming. The costs of the FEM calculation are substantially greater than shaft alignment calculation itself. As the result the hull deflections, in spite of their importance, are calculated very rarely. So simple methods for hull deflection estimation are still demanded.
For this reason the special module for the vertical hull deflections estimation is supplied with ShaftDesigner software. It is specially designed for mechanical engineers. It is enough to be able to read the ship hull structural drawings to use this module. Currently it can be applied to the ships with the engine room located at the aft part but in the future the module will be applied to the ships with arbitrary position of the engine room.
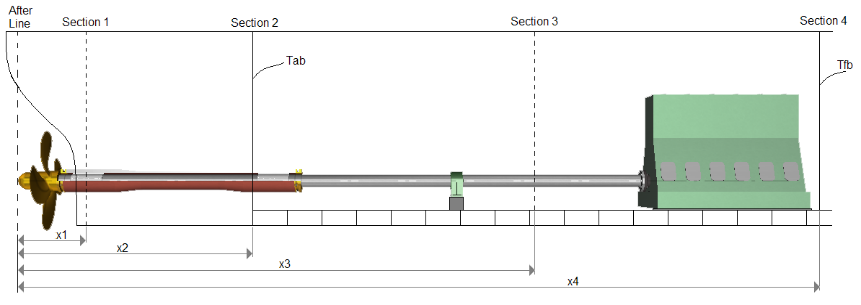
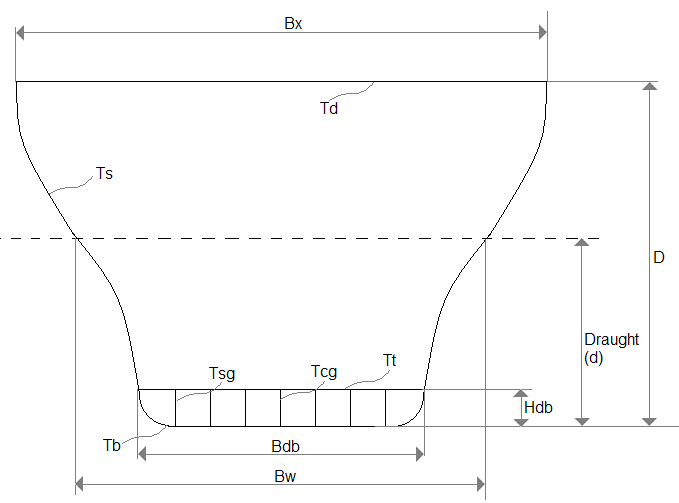
Figure 5: Input data for hull deflections calculation
The input data for hull deflections calculation include general information such as main scantlings, plate thicknesses for several ship hull sections. To take into account girders and longitudinals the effective thickness of the plates is introduced Fig. 5.
The double bottom parameters are taken into account as well. The algorithms of the hull deflection calculation were tested and proved by the full scale measurements.
The software calculates bearing deflection relative to the current reference line Fig. 6 as a sum of the deflections caused by the hull girder deformations, by the double bottom local deflections and by the bulkheads deformations. The sum is not absolute deflections but only the changes of the deflections that correspond to the ship draught deviations from the shafting alignment state.
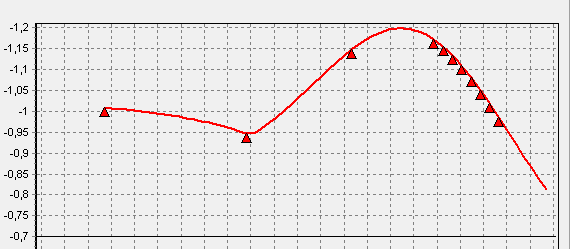
Figure 6: Calculated hull deflections
There are the situations when the shaft alignment works are to be performed in a dry dock. The approach to predict hull deformations after ship launching on the statistical base is well known [5]. Our experience shows that the hull deformations after the ship launching may be quite different even in the case of the sister ships. Therefore if the shaft alignment is to be performed in the dry dock, the shaft deflection should be calculated using the loads caused by the docking supports case by case.
5. PROPELLER LOADS
According to the Classification Societies requirements propeller loads, acting in the vertical and horizontal planes, Fig. 7 are to be taken into account in SAP design. They are significant enough especially for huge propellers of modern cargo ships. The propeller loads cause the edge loading and affect the lubrication condition of the stern tube bearings.
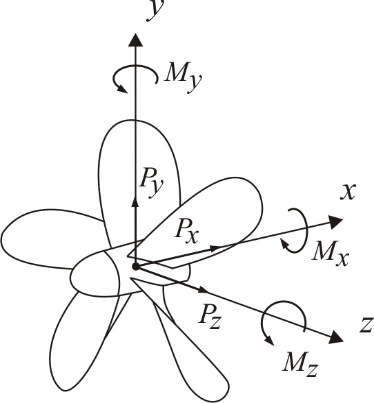
Figure: 7 Propeller load components
ShaftDesigner proposes five methods for propeller loads estimation of one screw ships depending on the scope of propeller information available:
- statistical;
- semi empirical;
- approximate;
- wake flow method;
- improved wake flow method.
All the methods are based on the known torque and thrust Px, Mx and provide the propeller hydrodynamic loads calculation for any level of the input information available.
The statistical method additionally requires the most general information regarding the propeller. Four unknown load components Py, My, Pz, Mz are to be calculated as a percent from Px and Mx. The percentages were estimated by application of wake flow method to the ships for which wake field information is known [6].
The semi empirical method is based on the propeller loads full scale measurements [7]. Some additional information concerning of the ship hull and propeller geometry is required for this method.
The approximate, wake flow and improved wake flow methods implement direct calculations based on the wake flow information. The approximate method uses interpolated wake flow of the nearest ships in the database. The wake flow method and improved wake flow method are based on the true wake field data of the specific ship measured during the towing tank tests. Moreover the improved wake flow method requires most detailed information from the propeller drawing.
Last two methods generate load distribution along the blade and calculate the integral hydrodynamic loads. Thrust point migrates along the eccentricity orbit during rotation of the propeller by the angle 2π/Z, where Z is blade number. Due to the thrust eccentricity vertical and horizontal bending moments arise.
Unfortunately there is no single universally recognized method of propeller load computation for the purpose of shaft alignment calculations. It is no wonder that most of Classification Societies rules do not provide any recommendation for this matter.
Obviously further theoretical and experimental studies are still needed to provide the shaft designers with reliable present-day information, particularly for two-screw ships. The latest progress of CFD and experimental techniques gives a hope that in the future the situation will be improved significantly.
| a) | 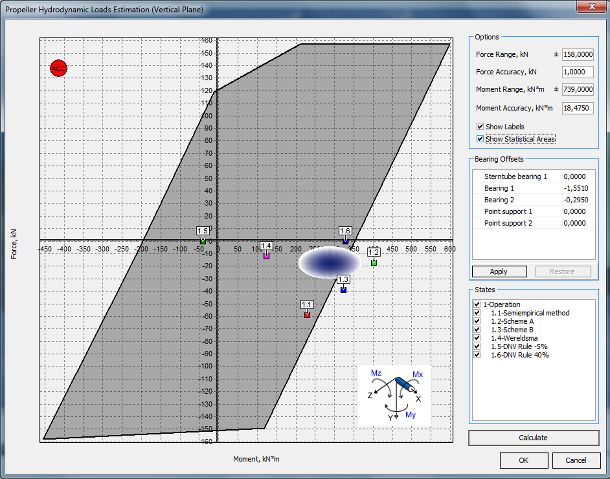 |
b) | 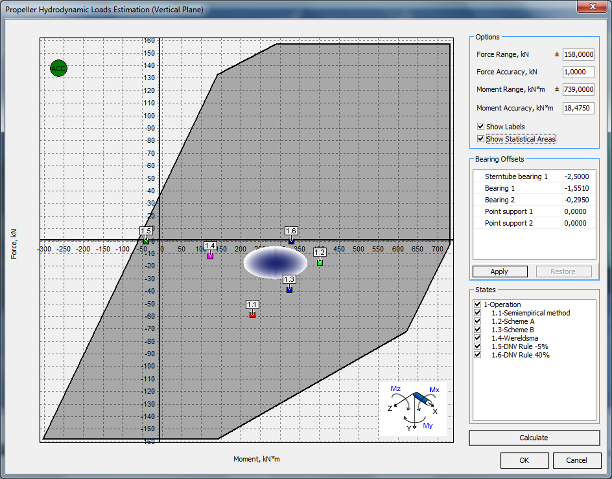 |
Figure 8: The allowable propeller loads areas depending on SAP
6. PARAMETRIC CALCULATIONS
The developed methods for hydrodynamic loads calculation have shown a great scatter of the results [6]. This makes the shaft designers unhappy; they lose the confidence that the acceptance criteria will not be violated in the operation if only one of the results for hydrodynamic loads is used in shaft alignment design.
When the required input parameters are not known exactly it is general practice to perform the parametric calculation. The parametric calculation is used in ShaftDesigner to validate the propeller loads.
The relation between shaft alignment acceptance criteria and the hydrodynamic vertical moment Mz and the vertical force Py can be visualized by means of a special propeller load validation diagram Fig. 8 showing the allowable propeller loads area (shaded) and inputted propeller loads (points and ellipse spot). The view of diagrams depends on the acceptance criteria and the specific bearings offsets as well.
To build these diagrams the parametric calculations were performed. Propeller hydrodynamic loads have been varied to build the border between allowable and not allowable areas.
As can be seen from Fig. 8a used SAP is not good because the propeller loads points (user input) are not located entirely within the allowable area. After the SAP has been changed estimated propeller loads focused at the center of the allowable area Fig. 8b and shaft designers feel more confident and do not care about the accuracy of the propeller load setting.
Another case of the parametric calculations application is checking of the acceptance criteria for the gearboxes. Sometimes the acceptance criteria, which are formulated by the gearbox manufacturer, are not compatible with the shaft line design and the ship operating conditions. In this case acceptable SAP cannot be found at all. To be sure that the appropriate solution can (or cannot) be found and avoid time wasting for non-productive calculations the special module for checking the gearbox acceptance criteria was developed.
| a) | 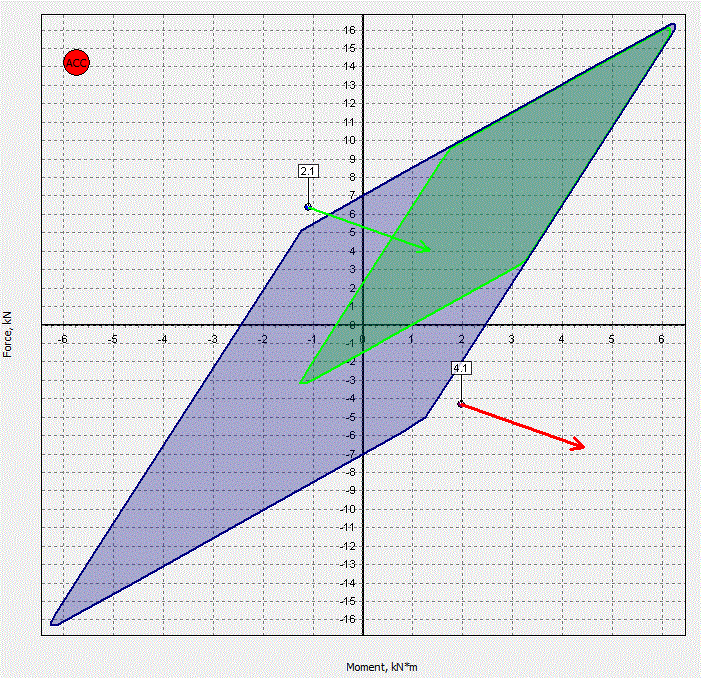 |
b) | 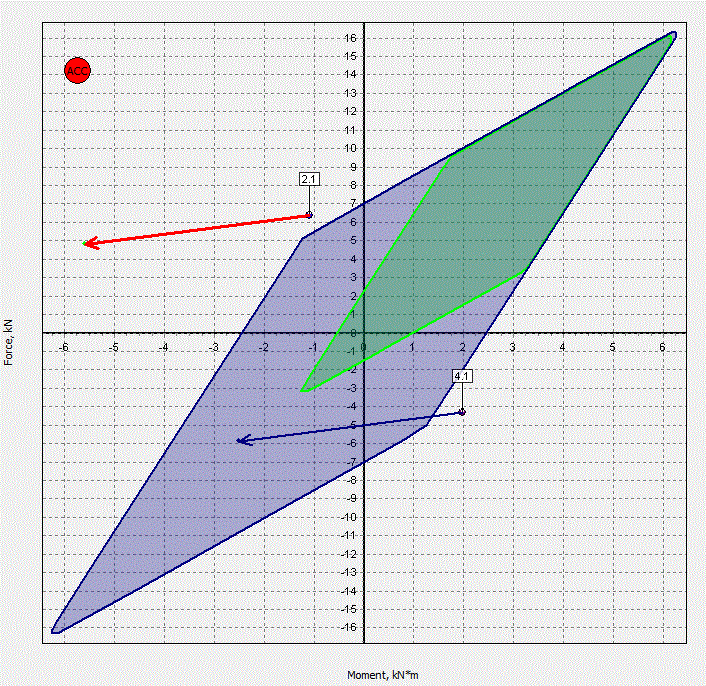 |
Figure 9: Contradictive gear box acceptance criteria cannot be satisfied simultaneously
The diagrams of allowable bending moment and the shear force at the gearbox flange obtained by the parametric calculations are shown on the Fig. 9. There is the case of two calculation states. The acceptable SAP exists if the vectors’ ends can be moved inside the correspondent allowable area. Otherwise the acceptance criteria are not compatible with the shaft line design. Starting points of the vectors indicate gear box flange loads at zero offsets. As can be seen from Fig. 9 gear box acceptance criteria are contradictive and in any case cannot be satisfied simultaneously.
It is much easier to perform the parametric calculations in many other cases when some parameters are not known exactly, e.g. bearing stiffness, than try to find exact values of the unknown parameters.
7. REVERSE ENGINEERING
Reversed calculations are the shaft alignment calculations intended to determine bearing offsets from the specific measured data. Such kind of calculations is indispensable for the ships under repair.
SAP design for the ship under repair differs from the SAP design for new building ship. For the new building ship all bearings are accessible and the calculated alignment parameters can be freely set for all bearings. For the repaired ship, when it is afloat, several bearings are not accessible (strut bearings, stern tube bearings). The offsets of these bearings cannot be changed anymore and it is very important to determine their values to provide the optimum shaft alignment parameters for the rest bearings. ShaftDesigner reverse engineering module is specially designed for this case.
As a rule one of the following shaft bending parameters are measured on board to control shaft alignment:
- Sags and Gaps at the open flange connections;
- bearing loads;
- jack-up test diagrams;
- bending stress at the check points;
- deflections of the shaft line.
Each of the parameters can be used for reverse engineering. Experienced shaft alignment companies combine measurements of different bending parameters to have more reliable results. For this reason the reverse engineering module of ShaftDesigner allows reversed calculations using data of different nature simultaneously, Fig. 10.
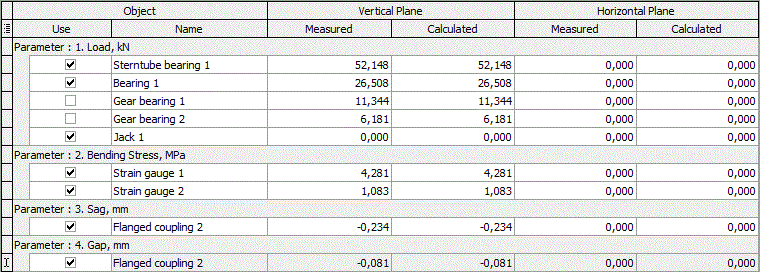
Figure 10: Parameters for reversed calculation
Strain gauge alignment technique becomes popular last years. This technique does not require the disassembling of the shaft line, but unlike the jack-up testing, allows aligning the shafts in the horizontal plain as well. Strain gauge alignment module uses the reversed calculation from the bending stress at the check points.
The measured bending stress or strain instrumentation readings are used to calculate the bearing offsets adjustments Fig. 11.
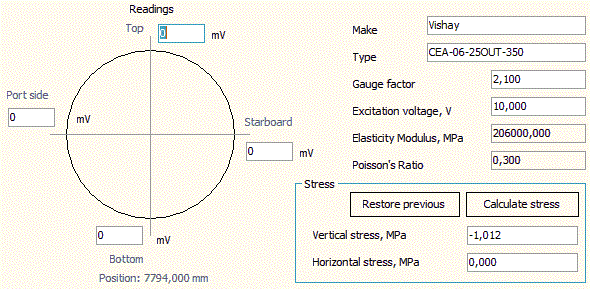
Figure: 11 Strain gauge alignment dialog window
To facilitate the process of the strain gauge alignment the bearing adjustments are visualized with the special shaft bending diagram.
In the cases when bearing adjustments in the horizontal plane is not required the good results may be achieved with the reversed calculations on the base of jack-up test diagrams. Actual vertical bearing offsets can be determined as the offsets that bring the best possible matching of measured and calculated jack-up test diagram, Fig. 12. Black solid line on the Fig. 12 is the shaft lifting branch, the black dashed line – shaft releasing branch, the theoretical result is shown by the red line.
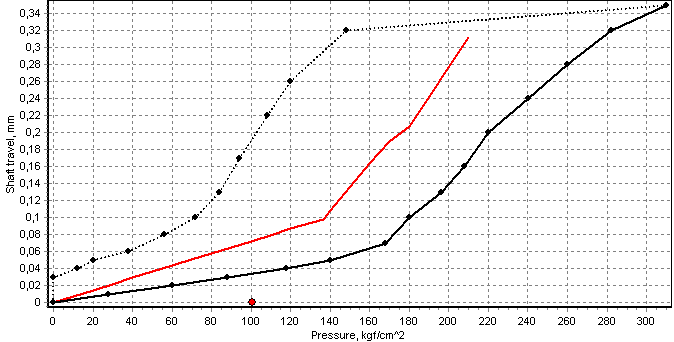
Fig. 12 Measured and calculated jack-up test diagram for the shaft line with high friction elements
8. SHAFT ALIGNMENT AND BEARING LUBRICATION
ShaftDesigner application includes the module for the calculation of bearing lubrication pressure. The calculated lubrication pressure is a result of the iterative process on each step of which Reynolds equation is solving by FEM method. Bearing bush in calculation is considered as absolutely stiff.
Finally the application builds lubrication pressure diagram Fig. 13. If the calculated lubrication film thickness in all operation conditions is greater than the minimal allowable thickness, the SAP design can be considered as satisfactory.
The calculation of the bearing lubrication pressure is time consuming process therefore it should be performed as a final checking of the SAP design.
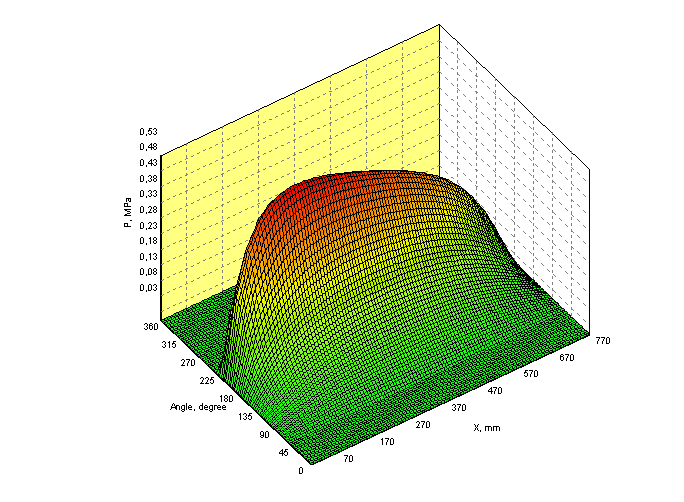
Figure: 13 Lubrication pressure for stern tube bearing
For the estimation of the bearing load capacity ShaftDesigner application includes special module for the fast lubrication pressure evaluation. It indicates is the build-up of bearing lubrication film possible at the specified shaft speed and shaft load conditions or not. This calculation is based on the minimum allowable lubrication film thickness, bearing static and shaft deflections that have been obtained in the static condition for non-rotating shaft.
According to the Stribeck-Hersey curve idea the bearings in the steady operating conditions must operate at Sommerfeld numbers that ensure hydrodynamic lubrication. Non-compliance with this requirement leads to the fast wear out of the bearing bush, loss of energy in operation.
Currently there is no commercial software on the world’s market that permits to build Stribeck-Hersey curve for the specific stern tube bearing. The investigations in this domain are at the beginning stage [8] but one thing is certain: the shaft alignment influences the lubrication condition very much.
It should be pointed that the bearing bush is not absolutely stiff. This assumption is not applicable to non-metal water lubricated stern tube bearings first of all. For such bearings the Elasto-Hydrodynamic Lubrication (EHL) problem must be solved because this type of bearing is very sensitive to the local overloading.
9. CONCLUSIONS
Almost two decades of practical experience with using a computer application for shaft alignment design for new building and repair projects led to the following conclusions.
- If the shaft alignment works are to be performed in dry dock the shaft deflection should be calculated using the loads caused by the docking supports. Computer application for the shaft alignment design should provide the possibility for the hull deflection estimation in this case.
- In spite of the importance of hydrodynamic propeller loads for the purpose of shaft alignment calculations there is no single universally recognized or standard method of the propeller load computation. Further theoretical and experimental studies for improving of model experiments, numerical modeling and full-scale measurements, particularly for two-screw ships, are still needed to provide the shaft designers with reliable present-day information.
- In the face of the input data uncertainty the parametric calculations in shaft alignment design are the practical tool that allows saving time and money and avoiding the research or calculation of exact input data.
- The shaft alignment design for the repaired ships, when the part of the bearings have unknown fixed offsets, requires performing the preliminary investigations of the actual bearing position. The reversed shaft alignment calculations are the single way that allows doing this.
- The shaft alignment plan may be considered as an acceptable if it provides hydrodynamic lubrication for the stern tube bearings in the main operating conditions. ShaftDesigner provides not only the procedure for the hydrodynamic pressure calculation but allows fast bearing load capacity evaluation for the shaft alignment plan checking. In the future EHL problem solving module must be added to the shaft alignment application to calculate lubrication pressure of non-metal stern tube bearing. Additionally free shaped bearing bush models should be used to have the most realistic results.
10. ACKNOWLEDGEMENTS
This work would not been possible without the support of SKF Marine Service Center.
11. REFERENCES
- VOLCY, G. C., ‘Memoirs of Marine Troubleshooter’, The Institute of Marine Engineers, London, 1995.
- BUREAU VERITAS, ‘Elastic Shaft Alignment (ESA)’, Rule Note NR 592 DT R00 E, June 2013.
- DET NORSKE VERITAS, ‘Rules for Ships / High Speed, Light Craft and Naval Surface Craft’, Pt.4, Ch.4, Sec.1, January 2013.
- BATRAK, Yu., ‘New CAE Package for Propulsion Train Calculations’, International Conference on Computer Application in Shipbuilding, Papers Vol. II, 1-3 September 2009.
- SVERKO, D., ‘Effect of the Hull Deflections on Propulsion System Bearing Loading’, Proceedings of 25-th CIMAC Congress, Paper No 236, Vienna, 2007.
- BATRAK, Y., SHESTOPAL, V., ‘Propeller Hydrodynamic Loads in Relation to propulsion Shaft Alignment and Vibration Calculations’, Propellers / Shafting 2012 Symposium, Norfolk VA,11-12 September 2012.
- TECHNICAL REPORT, ‘Semi empirical method for estimation of hydrodynamic bending moments applied to the propulsion shafting of single-screw ships with a conventional aft end shape’, Krylov Institute, Report No 16077, 1973. (In Russian.)
- KRAKER, A., VAN OSTAYEN., RIXEN, D.J., ‘Calculation of Stribeck curves for (water) lubricated journal bearings’, Tribology International 40, 2007.
12. AUTHORS BIOGRAPHY
Dr. Yuriy Batrak Ph.D holds the current position of consultant at Intellectual Maritime Technologies company. He is responsible for the formulation of the software development trends. His previous experience includes developing of ShaftMaster software for shaft alignment calculations, lectures on computer science and mathematics at the university, hull structure tests at the shipyards, sea trials measurements.
Roman Batrak holds the current position of project manager at Intellectual Maritime Technologies company. He is responsible for general managing of software development, application programming, automatic testing and software protection. His previous experience includes development of the software system for ship traffic control in channels.
Dmytro Berin holds the current position of programmer at Intellectual Maritime Technologies company. He is responsible for optimization procedures programming, programming of GUI and calculation results documentation. His previous experience includes development of the software system for ship traffic control in channels.
