Dr. Yuriy Batrak, October 2019, Intellectual Maritime Technologies, Ukraine
Otto von Bismarck told the story after his visit to Saint Petersburg, Russia in 1859.
“During the first spring days, it was then the custom for everyone connected with the court to promenade in the Summer Garden between Paul’s Palace and the Neva. There the Emperor had noticed a sentry standing in the middle of a grass plot; in reply to the question why he was standing there, the soldier could only answer, ‘Those are my ordered.’ The Emperor, therefore, sent one of his adjutants to the guard-room to make inquiries; but no explanation was forthcoming except that a sentry had to stand there winter and summer. The source of the original order could no longer be discovered. The matter was talked of at course and reached the ears of the servants. One of these, an old pensioner, came forward and stated that his father had said to him as they passed the sentry in the Summer Garden: ‘There he is, still standing to guard the flower; on that spot Empress Catherine [1729-1796] once noticed a snowdrop in bloom unusually early and gave orders that it was not to be plucked.’ This command had been carried out by placing a sentry on the spot, and ever since then one had stood there all the year-round.”
Some Classification societies are doing something like that. They once have included the requirement to submit bearing influence coefficients (influence numbers) in propulsion shafting alignment calculations in their Rules and continue to do this until today.
Bearing influence coefficients concept arose more than 60 years ago when the bearings in shaft alignment calculation treated as a simple absolutely stiff support with prevented shaft-bearing disconnection. In such conditions the calculation system is linear and influence coefficients worked properly to define changes in bearing loads corresponding to small bearing offsets. But today the calculation system lost linearity because in shaft alignment design an extended support model of bearing became commonly used. The extended support has no single point of contact; shaft disconnection with bearing bush is possible, bearing bush deflection may happen, etc. It means that bearing influence coefficients concept is no longer applicable to modern models. Using such model the shaft designers nolens volens violate this Class requirement to submit bearing influence coefficients. Why this requirement is still included in the Class Rules without any qualification?
It should be noted that the situation with the bearing influence coefficients is not much better when the point supports are used to model bearings. It is well known that bearings in shaft alignment design should not be considered as absolutely stiff. Bearing stiffness consists of two components: an internal stiffness and an external stiffness. The internal stiffness includes bush stiffness, bearing case stiffness and stiffness of other bearing internal elements which move together with bearing case. The external stiffness is the stiffness of bearing stool or other support structures. A specific feature of these support structures is a displacement of their base in operation caused by hull deflections thereby causing bearing case displacement.
As stated above the bearing influence coefficients matrix was introduced at the beginning for the absolutely stiff supports. In this case, the bearing influence coefficients matrix is symmetrical. Since those days, most are convinced that bearing influence coefficients matrix is always symmetrical. But this is not so.
Let us consider simple shaft supported by bearings installed on flexible stools which in turn installed on the flexible double bottom. Thus the bearings having internal and external stiffness can be displaced due to oil film build-up, bearing thermal growth or double bottom deflection.

Let us consider bearing influence coefficient matrices for this shaft calculated using different approaches concerning of bearing stiffness.
- Shafting supports are absolutely stiff.

The bearing influence coefficient matrix is symmetrical.
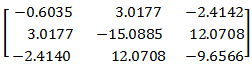 2. Both internal and external stiffness of not displaced bearing is taken into account.
2. Both internal and external stiffness of not displaced bearing is taken into account.

In this case, the matrix of shaft points displacement influence coefficients is NOT symmetrical.
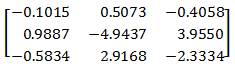 3. Both internal and external stiffness of not displaced bearing is taken into account. For the displaced support only the internal bearing stiffness is taken into account (bearing case is displaced).
3. Both internal and external stiffness of not displaced bearing is taken into account. For the displaced support only the internal bearing stiffness is taken into account (bearing case is displaced).

Bearing influence coefficients matrix for bearing case displacement is NOT symmetrical.
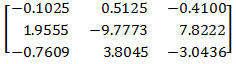 4. Internal and external stiffness of all bearings, including that, is displaced, is taken into account (hull deflections influence coefficients).
4. Internal and external stiffness of all bearings, including that, is displaced, is taken into account (hull deflections influence coefficients).

Bearing influence coefficients matrix for hull deflections is symmetrical.
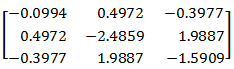
As can be seen, these bearing influence coefficient matrices differ not only by symmetry but have different values of coefficients.
The question is which the bearing influence coefficient matrix do the Classification Societies want to see?
However, you should not think that bearing influence coefficient matrices are useless. They are a very useful tool when two different models of the same propulsion shafting should be compared. The comparing of corresponding matrices, calculated using identical approach, allows revealing differences between the models’ data.
